 It’s a bit off-topic for the series, but I can’t even go to Google now without being reminded of the World Cup and soccer this, soccer that. (Apologies to non-Americans who know the sport as football—but don’t get me started on football!) I have often wondered: given characteristic low score values, is soccer anything more than Poisson noise? When discussing this with colleagues, one pointed me to this XKCD comic, reproduced at right.
It’s a bit off-topic for the series, but I can’t even go to Google now without being reminded of the World Cup and soccer this, soccer that. (Apologies to non-Americans who know the sport as football—but don’t get me started on football!) I have often wondered: given characteristic low score values, is soccer anything more than Poisson noise? When discussing this with colleagues, one pointed me to this XKCD comic, reproduced at right.
Any random process that produces discrete events in some time interval, with uniform probability per unit time follows a Poisson distribution. When the number of events becomes large, the distribution tends toward a Gaussian (normal) distribution.
My thesis is that soccer is an amalgam of random processes whose net effect produces rare events—those more-or-less unpredictable events spread more-or-less uniformly in time. Whether a good or bad bounce off the bar, a goal keeper who may or may not prevent a goal, a referee who may or may not see an illegal action, a pass that may or may not be intercepted, and on and on: the game is full of random, unpredictable events. So I expect soccer to behave similarly to a Poisson process and follow a Poisson distribution. By extension, I will claim that the attention devoted to the World Cup is founded on flimsy numerology and might even be called a tremendous waste of time and money.
Normally I allow comments on Do the Math for ten days after each post. I’ve tackled some controversial topics and stirred up emotional responses. Yet I predict that the outrage generated by my insinuation that watching soccer is a waste of time will absolutely dwarf the reactions to my saying that we may not be looking at a space-faring future, or that indeed we may face collapse of civilization. To the extent that this (untested) prediction is true, it would seem that soccer is more important than the fate of the world, in the eyes of many. Scary, if true. [After reconsideration, I enabled comments, but I won’t have time to vet and respond with my usual level of attention.]
But getting back to soccer numerology, my question becomes: given a final score (which is taken to be the ultimate “truth” of the match) how likely is it that the victor is actually a better team?
Expectations and Subtleties
One could imagine other measures of a team’s prowess in a game besides final score, like how many shots on goal, what fraction of the time a team’s offense keeps the ball downfield, how many goals the keeper directly prevented, etc. But it’s the final score that dictates the fate of the team in the series. So I’ll go with the measure that has actual consequences and most directly influences the high emotions of the fans.
But what is the truth of the situation? If team A were to play team B many times, what would the outcomes be? In this hypothetical situation, we want to compare the teams as they are at one moment in time, ignoring fatigue, changes in roster, injuries, evolving strategies, etc. that would happen if we actually had the teams play many games in series. What I’m after is a measure of the capabilities of the team at an instant in time: a snapshot. We will characterize this as the expectation value, or XA for team A and XB for team B. These measures can be thought of as the average score the team would acquire in repeated trials (matches), and in general will not be confined to integers, like the actual scores are.
Now, the value XA is not a universal characteristic of team A. It’s only valid when playing team B. If a World Cup team (A) played a high school team (B), we would not be surprised by a score of 83 to 0, and if played multiple times, we may find that XA = 68.3 and XB = 0.7. Each instance would produce random numbers near these averages. But if the same team (A) plays another World Cup team, we might see XA = 2.3 and XB = 1.9, so that a 2:2 tie would not surprise us. Then when team A encounters World Cup team C, we might find that XA = 1.3 and XC = 0.8. While team A will still often prevail against team C, perhaps team C’s defense is able to shut down team A’s offense more effectively than is the case for team B. Different strengths and weaknesses make the expectation values depend on the particulars of the match-up. And we can’t necessarily apply transitive properties. For instance, we could have XA>XB when A plays B, XB>XC when B plays C, yet XC>XA when A plays C—based on the peculiarities of cross-team “chemistry.” And even XA compared to XB could change over time if the teams actually played each other multiple times in a series or season.
All this is to say that I get the subtleties (at least some of them). I am not saying that I can reduce the entire sport to algorithmic expectations. That’s why I want to focus on a particular game resulting in a particular score. Given that there are some “true” expectation values for that match-up, how much meaning can we place in the final score given random fluctuations?
Poisson Statistics
First, a look at the math of Poisson statistics. If I have an expected (average) outcome of X (traditionally labeled &lambda), what are the chances that in a given trial (game) I get N as a result, where N is an integer? Under Poisson statistics, the answer is:
p(N) = XNe−X/N!
where e represents the exponential function, and N! is N-factorial, or N(N−1)(N−2)…1 (e.g., 4! = 24). Some relevant examples appear in the table below.
| N | X=0.7 | X=1.0 | X=2.0 | X=2.4 |
| 0 | 0.496 | 0.368 | 0.135 | 0.091 |
| 1 | 0.348 | 0.368 | 0.271 | 0.218 |
| 2 | 0.122 | 0.184 | 0.271 | 0.261 |
| 3 | 0.028 | 0.061 | 0.180 | 0.209 |
| 4 | 0.005 | 0.015 | 0.090 | 0.125 |
| 5 | 0.001 | 0.003 | 0.036 | 0.060 |
| 6 | 0.000 | 0.001 | 0.012 | 0.024 |
Each column (when extended to all N) sums to 1.0, as probability should. Note all “teams” above may score zero by chance, even if “expected” to score 2.4 in a game. Sure, the probability of zero is reduced to 9% for the X = 2.4 team, but it will happen. The point is that the Poisson distribution is pretty spread out, but in a sensible way: the team with an expectation of 0.7 has essentially no chance of scoring 6 by dumb luck, while the 2.4 team (coincidentally) has a 2.4% chance of doing so.
We can turn the Poisson distribution around, and ask: if a team scores N points, what is the probability (or more technically correct, the probability density) that the underlying expectation value is X? This is more relevant when assessing an actual game outcome.
An example appears in the plot below. The way to read it is: if I have an expectation value of <value on the horizontal axis>, what is the probability of having 2 as an outcome? Or inversely—which is the point—if I have an outcome of 2, what is the probability (density) of this being due to an expectation value of <value on the horizontal axis>?
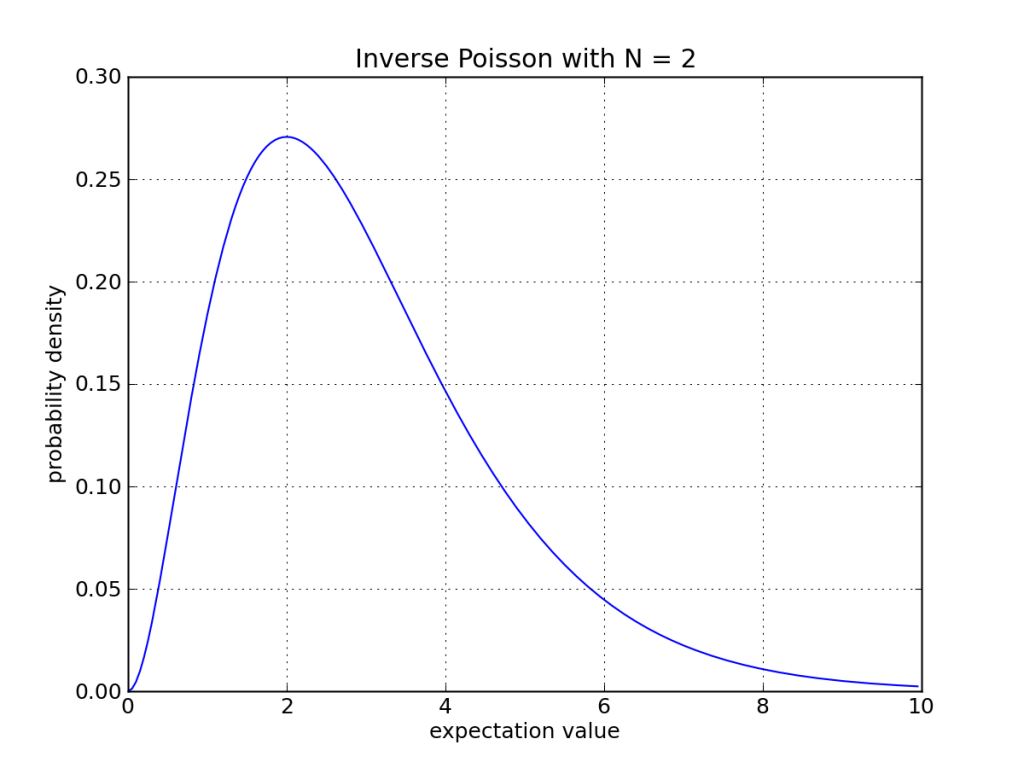 Example Application
Example Application
By applying this inversion to both teams’ final scores, we can assess the frequency that the winning team is actually better (i.e., has a higher expectation value) than the losing team. We form a two-dimensional parameter space comprised of all values of XA and XB, and for each one can assess the joint probability of getting the score N to M. The joint probability is found by multiplying the individual probabilities. Figuring joint probabilities in this way assumes independence of the two scores, which is certainly open to criticism. Don’t mistake this independence for claiming that the teams have no effect on each other: the expectation values embody this dynamic, and are particular to the match-up. This independence is basically saying that the expectation values do not change as a result of how many goals the other team winds up scoring in the game. Maybe a team is galvanized by the others’ score, or maybe demoralized. This would impact independence, but I can think of lots of scenarios in which it would go either way, so will not bias in one particular direction.
If you’re on board and keen to see the results, skip ahead. But if you still want a feel for how this scheme works in practice, an illustrative table appears below for the case of a 2 to 1 final score.
| X vals | 1 | 2 | 3 | 4 | 5 | totals |
| 1 | 6.77 | 4.98 | 2.75 | 1.35 | 0.62 | 16.47 |
| 2 | 9.96 | 7.33 | 4.04 | 1.98 | 0.91 | 24.22 |
| 3 | 8.24 | 6.06 | 3.35 | 1.64 | 0.75 | 20.04 |
| 4 | 5.39 | 3.97 | 2.19 | 1.07 | 0.49 | 13.11 |
| 5 | 3.10 | 2.28 | 1.26 | 0.62 | 0.28 | 7.54 |
| 6 | 1.64 | 1.21 | 0.67 | 0.33 | 0.15 | 4.00 |
| 7 | 0.82 | 0.60 | 0.33 | 0.16 | 0.08 | 1.99 |
| totals | 35.92 | 26.43 | 14.59 | 7.15 | 3.28 | 87.37 |
The winning team’s expectation value increases along the left hand side, and the losing team’s expectation value runs along the top. This table captures 87% of the possibilities; had I extended in both directions (to larger expectation values) and sampled less coarsely, we would have gotten 100%. The way to interpret this table is that if the final score was 2 to 1, the chances that the expectation values were actually 2 vs. 1—in line with the final score—is 10%. The chances that the roles are reversed, and the expectation values were 1 vs. 2 is 5%. There is a 2% chance that the losing team had an expectation of 4 while the winning team had an expectation of 2, making this a dramatic upset. The most probable “truth” is an expectation of 2 vs. 1, in accordance with the actual score. Looking at the totals, the most probable expectation for team A (winner) is 2, while for team B the most likely expectation score is 1—again in accordance with expectation.
If we sum the probabilities in the table where the winning team’s expectation is indeed higher than the losing team’s (correct game outcome), splitting the probabilities when the expectations are matched, we get 58.5% (though out of 87% total, so we might expect about 67% if we had extended the table. The implication is that a 2 to 1 score is correctly interpreted as a statement of dominance two-thirds of the time.
Calculated Results
But the above example is a bit coarse-grained. A more thorough exploration of parameter space would include fractional expectation values. So get ready for the full deal. In the table that follows, each row represents a score for a non-tie game (from which all we can conclude is that each team has a 50% chance of being better than the other). Following are percent chances that the winning team is truly better than the losing team. The second column examines every expectation value between 0 and 16 in steps of 0.01, uniformly weighted. That’s 1600 cases for each team, for a total of 2.6 million test cases. You’ll forgive me for not including the table associated table this time. It does not pay to extend beyond expectations of about 16, because the Poisson inverse probability is pretty much dead by this time.
| Score | Uniform | μ=1.5, σ=2.0 | μ=2.0, σ=2.0 | μ=2.0, σ=1.5 |
| 1 to 0 | 75.1 | 73.1 | 72.7 | 71.2 |
| 2 to 1 | 68.7 | 66.4 | 66.1 | 64.9 |
| 2 to 0 | 87.6 | 84.7 | 84.3 | 82.4 |
| 3 to 2 | 65.6 | 63.3 | 63.1 | 62.1 |
| 3 to 1 | 81.2 | 77.6 | 77.2 | 75.4 |
| 3 to 0 | 93.8 | 91.1 | 90.7 | 88.9 |
| 4 to 3 | 63.7 | 61.4 | 61.2 | 60.4 |
| 4 to 2 | 77.3 | 73.5 | 73.1 | 71.6 |
| 4 to 1 | 89.1 | 85.1 | 84.7 | 82.8 |
| 4 to 0 | 96.9 | 94.7 | 94.4 | 92.9 |
| 5 to 4 | 62.3 | 60.1 | 59.9 | 59.3 |
| 5 to 3 | 74.6 | 70.7 | 70.4 | 69.0 |
| 5 to 2 | 85.5 | 81.0 | 80.6 | 78.9 |
| 5 to 1 | 93.7 | 90.1 | 89.7 | 87.9 |
| 5 to 0 | 98.4 | 96.8 | 96.5 | 95.4 |
| 6 to 5 | 61.2 | 59.1 | 59.0 | 58.4 |
| 6 to 4 | 72.5 | 68.7 | 68.4 | 67.2 |
| 6 to 3 | 82.8 | 78.0 | 77.6 | 76.1 |
| 6 to 2 | 91.0 | 86.6 | 86.1 | 84.4 |
| 6 to 1 | 96.5 | 93.5 | 93.1 | 91.6 |
| 6 to 0 | 99.2 | 98.0 | 97.8 | 96.9 |
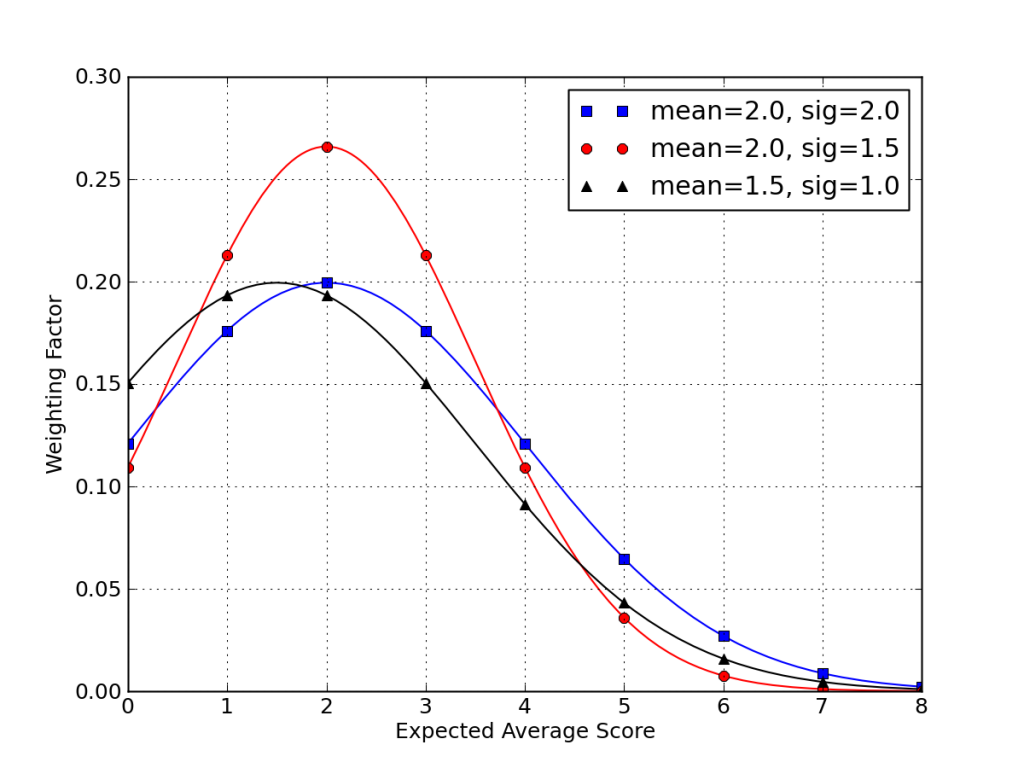
So far, we have considered no prior information on likely expectation values for a team. We have let the low scores effectively kill the chances of the actual expectation being very large (it would be unlikely indeed for a team with XA = 45 to end up scoring 3 points in a game). So the calculation converges without needing to assume any priors. But we can do better than this. We already have a sense for typical soccer game scores. We can model this reasonably with a Gaussian distribution whose mean, μ might be around 2, and whose standard deviation, σ, may be similar. Such a distribution would slightly disfavor a team’s average score from getting too low or too high.
Three test-case distributions for a team’s expected average score, XA, appear in the plot below.
The final three columns in the huge table above correspond to these three cases. What we find is that the probability of the winning team actually being better is not terribly sensitive to any weighting we might apply to favor “reasonable” expectation values. In general, the reliability of final scores correctly picking the winner decreases when “realistic” expectation values are considered.
Therefore, given a final score, you can look at this table and see how meaningful the score is in the face of Poisson statistics. A 3:2 score gives the winning team only a 5-in-8 chance of actually being a better team—in the absence of any additional information. But that’s the criterion for advancing: the score is paramount, and no other considerations are entertained.
Reflection
Personally, I don’t find this to be very impressive. Even a 6:1 blowout leaves a 7% chance that it was a statistical fluke. More typical scores are even less decisive.
Maybe some force within the game operates to squelch Poisson variation. This can be true in sports where a scoring event on the part of one team gives control to the other team for a time. But control flips back and forth so many times in soccer that it’s hard to spot a mechanism that kills statistical variation. It’s a good random machine. Sure, you can have a team whose offense is not often in control of the ball. This (and other factors) may suppress the expectation value, but does it remove the randomness? I would be skeptical.
Admittedly, I don’t follow soccer—in part because I suspect it boils down to watching well-executed random events. It could be that team A beating team B by 2:1 is a pretty repeatable event. What I have seen (and I have been to a World Cup game) seems to amount to a series of low-probability scoring attempts, where the reset button (control of the ball) is hit repeatedly throughout the game. I do not see a lot of long-term build-up of progress. One minute before a goal is scored, the crowd has no idea/anticipation of the impending event. American football by contrast often involves a slow march toward the goal line. Basketball has many changes of control, but scoring probability per possession is considerably higher. Baseball is a mixture: as bases load up, chances of scoring runs ticks upward, while the occasional home run pops up at random. Alas, for soccer, I can’t easily get past the smell of Poisson.
Oh geez: now I’ve wasted time on the World Cup too!
Hits: 1534
With some trepidation, I am turning comments on, to see what happens. I do not expect to spend much (any?) time reading or responding to comments. I’ll keep obvious trash (and inappropriate behavior/abuse) out, but otherwise feel that I’ve spent enough time on this topic already.
The post here (I don’t know if html in comments is allowed with your site): http://blog.wolfram.com/2014/06/20/predicting-who-will-win-the-world-cup-with-wolfram-language/ might be of interest to you in this regard. While I don’t know, of course, I’d speculate that you’re at least passingly familiar with Wolfram and Mathematica. As to a waste of time, yes, but I do follow “my” teams in (US type) football and baseball.
I fully agree with your analysis. In fact, I would go further; sports outcomes are statistically insignificant by design.
What I mean is this: in many sports leagues, the rules are designed to keep the teams as balanced as possible (e.g. lower-rank teams being given first-pick of new players). The overall intent is to keep the game “interesting” (and thus lucrative) by having matches be “close calls” and so on. If one allowed technical prowess to accrue and concentrate, some teams would dominate so severely that it would become boring. Overall, the intent of the organizers is to keep the matches close and unpredictable; to make them fun. But this inherently means that the outcome of a season is a poor measure of actual ranked team quality: the results are statistically insignificant by design.
This isn’t to say that all sports are equally random. Single-elimination tournaments are very bad at identifying the “true rank”, but rigorous round-robin style tournaments are much better. Some sports have more randomness than others. Competitions like the World Cup or the Olympics, where each faction is putting forth their absolute best team, at least don’t suffer from some of these ‘artificial levelling’ effects.
And yet, when matching-up extremely competent athletes in a very small number of trials (as is the norm in all professional sports), the outcome will always be mostly random, as you point out. (The uncontrolled random variation is a much larger signal than the minor variation in athlete/team abilities; to average-out that variation would require much more sampling.) In some sense, this is fine: if people enjoy watching it, so be it. But it does annoy me that people ascribe so much significance (and misplaced pride) in the outcome of a weighted random number generator.
It may be true in sports leagues in the USA, but football around the world doesn’t have drafts and salary caps. So the best teams keep getting better and poorer teams poorer. The UEFA Champions League was seen as a way of extending competition to more “worthy” clubs, but all that has done is allow the richer clubs to hoover up more resources to maintain the status quo.
I understand that Americans are a bit pissed that nobody cares much about their “football” (were the ball is egg shaped, usually handled by hand, and the players look like playmobil warriors when seen in between commercials 😉 )
But one can also consider the thing as below :
1) Let’s assume that a pro soccer team playing a truly amateur one would trash them (make the amateur team as amateur and unfit as you see fit)
2) then clearly the Poisson modelization doesn’t work on above game
3) then raise the level of the amateur team
4) when does your model starts working ?
note : I’m from a football playing country (France) although not a major fan, and somehow agree with you that the usually low number of goals can have as a result that the final score doesn’t reflect the teams “strength level” as straightforward as in other games, but that’s also part of it, also making the stance between attacking and defending very critical.
I suspect your point 2 is wrong. The pro vs amateur example just has a very high expected score for the pro team and a very low probability of an upset. The model works across the whole range of skill possibilities.
I had a hypothesis that the sport of basket ball would be virtually unchanged if the game was started with just 45 seconds on the clock. I think I am sitting close to Tom in the sports fan spectrum.
Thanks for the chuckle.
I would say that the Poisson approach applies no matter how unbalanced the team. It’s just that the expectation scores get to be very large numbers. You would not, for example expect the dominant team to score 74 points every time it played the high school team: there would be variation. In this case, the variation would not be enough to ever expect a different outcome (winner), but that’s not what Poisson statistics implies: just that an individual instance has (predictable) variation.
Here in Australia (and in UK too) there is a lotto type gambling game called the Pools, where the winning numbers are based on the results of soccer matches instead of the random draw of numbered balls. In order for this to work the soccer match results must be unpredictable to a large degree, for all practical purposes matching the random draw of numbered balls.
However, suggesting the World Cup may be a waste of time and money is a bit of a stretch. The fanatical fans who travel long distances to attend the venues spend millions (of whatever currency you choose) and the TV rights are worth millions too. The spectators are getting their emotional batteries recharged, as they would with any other spectator sport. After all, if the result was predictable, there would be no point in playing at all, would there?
Isn’t it irrelevant whether or not football/soccer/sports-in-general are important in some objective sense? It is objectively true that subjectivity is enormously important to the human animal and to human societies. Anyhow, another feature of people, which seems to me pretty objectively true even if I can’t cite to actual research (where by “can’t” I mean won’t bother to try), is that we are hardwired to seek out patterns, including the patterns in the form of narratives, as XKCD puts it. And we like narratives! And we like to spend time engaging with things that we like! QED… World Cup. But then, some few of us like the narratives we get from good old Tom, even more than from soccer, so keep it coming.
I think Stephen Jay Gould had essays on this sort of thing, baseball runs as statistical artifacts and such, or why a general rise in quality mean you’d never see .400 batting averages again. I don’t recall details, though.
Your idea is intriguing. But, ala what kebes says above, the World Cup *is* a bunch of round robin games at this stage, so we can perhaps test your idea. I note that so far, the results https://en.wikipedia.org/wiki/2014_FIFA_World_Cup#Group_A mostly seem consistent with a story that some teams simply are better than others, with most of the groups falling into a well-ordering. Only Group G looks badly circular, with Germany >> Portugal = USA > Ghan = Germany.
OTOH the 2010 results look a lot more ambiguous to my eye. I think I read that this year has seen far fewer draws than usual.
I would not claim that some teams are not better than others, or that the winner is randomly selected: just that sampling “noise” can produce unexpected (misleading) results. So the final score is not in itself an iron-clad indicator of the better team. Meanwhile, the better team is more likely to win a particular game. The scoring results are not meaningless, just unreliable.
A few years back, I read a piece by some guy who suggested that soccer is more exciting than some other games precisely _because_ its results are more random than in other sports. Who wants to spend hours watching a predictable victory unfold? I don’t care for spectator sports either way, but I found the idea intriguing.
I’m a mathematician and appreciate that spectator sports are little more than random number generators. But even that doesn’t seem like the real silliness: whether or not it’s random or deterministic, or reveals some deep truth about the ability or quality of either team, you have the fact that your emotional state is affected by a bunch of guys running around a field in Brazil. (Or not.)
It’s totally silly. But I still watch and enjoy it. (Or not…)
Fair point, and many of the comments above and below speak to a similar love of sports independent (or even due to) the random element. I have no problem with that.
What I do like about soccer and other physical sports is that it takes place in the 3-D world ruled by physics. I respect the control over trajectories, anticipation of bounces, and all those intricate “calculations” the practitioners must exercise by gut feel in split seconds. I would far rather throw a real ball around than emulate the experience in a virtual environment, for instance.
I’m not sure your data supports your anti-soccer conclusion. The most common soccer scores are 1-0, 1-1, 2-1, 2-0, 0-0 (10%), followed by 1-2, 3-1, 3-0, 2-2 (5%), accounting for 70% of all games. If we only include the subset of these scores in which a team wins, the mean probability that the winning team is actually the better team according to your table is 80%. If the best team needs to win 7 games to win the world cup, then they have a .8^7 = ~20% chance of winning the world cup. But consider that the worst team has literally almost no chance of winning. So we have a gradient from worst to best, where the best team is most likely to win, despite only winning 20% of the time. We have 64 years of continuous world cups every 4 years, so we can look at the stats. We expect the best team to have won ~20% of the 16 games played since 1950 which is 3.2 games. Brazil has won 4 and Germany 3. Seems about right.
I like it! You have a 2:1 score listed as both 10% and 5%, and I get 75% when weighting the non-repeating entries above. But anyway, yes: you’re point is good all the same. Stronger teams are more likely to win the series, and I could believe something in the ballpark of 20% is reasonable.
“One minute before a goal is scored, the crowd has no idea/anticipation of the impending event.” – this isn’t really true.
While it’s pretty difficult to predict the precise moment that a goal could come, because progress down the pitch can be extremely rapid, it’s certainly very common to feel that a goal is coming for five/ten minutes beforehand. The crowd definitely knows it too – they go quiet when nothing’s doing (and yes, occasionally there will be a mistake and a goal is scored) and get very loud when there’s some very sustained pressure.
World Cup football is probably not the ideal venue for this kind of analysis – it is literally a different league to the normal game.
I have nothing in this either way, and I did enjoy your analysis, but I agree with Alex. Many times in American football nobody know who will score 1:00 minute before it happens.
I might be completely missing the point (haven’t studied probability since 1998) but go on then, tell me who’s going to win the World Cup. Or just Croatia vs Mexico, which starts in a few minutes.
Unless you can do that fairly accurately then I don’t see why you’re picking on football. Surely life is just random events, some executed better than others!
Yes, you are missing the point.
He’s not saying that the result is the opposite of predictable and thus the strength of the two teams has no bearing. It doesn’t make sense for you to ask him to predict the result of a game because he is agreeing with you.
The fact that soccer has such a large random element means that even fairly weak teams have a chance of beating very strong teams. And that’s precisely what makes it such fun to support.
The pleasure in watching it is not in seeing massive, deterministic scores. Most games are an exercise in drawn-out foreplay, with beautiful sequences that fall apart. A large element of those amazing passes, free kicks, goals etc. comes down to chance, but the skill of the players involved make them more likely to occur. In any case, they’re awesome to behold.
All in, I think you’re looking for something out of soccer which is different from what soccer fans look for in soccer.
(I call it soccer because in Ireland, a different game is called football.)
Hi,
in the second paragraph in “Expectations and Subtleties” you mention the paradigm, which is in my view wrong. If we could really could repeat a game under the same circumstances, you would be right. But Players have not always the same competence or power. heck, they age, therefore their skills will never be constant.
But i’m sure, with time, you really could predict the outcomes, due to similar skillsets between players. Though it would kill the sport. But perhaps.. that would be nice 🙂
Hey, nice post!
Being a fútbol fan I can not be more in the opposite side of the field but I understand your point.
I think USA people have the need of predicting (or knowing) how things are made, same as UK people, USA people need a clear way of penalizing bad actitudes and rewarding good ones. The lack of those things in fútbol hurts the very soul of the North Americans and prevents them of enjoying the sport.
Fútbol on the other side embraces improvisation and is not always rewarding the good ones (the best ones), Maradona won a World Cup almost by himself, a bad team always has some chance of winning. There is no meritocracy on fútbol and fútbol fans are aware.
The only difference between you and me (I’m just guessing of course) is that I can live with that, I know my team is not always gonna win even if it is a very good team and when playing with better teams I know I have some decent chance.
Thanks, and sorry for my crappy english!
Gabriel
Very interesting point, and similar to what Barry said above. Besides a North American mindset, perhaps I am also offended as an experimentalist in that a single game is not a reliable experiment to determine a winner. Plenty of scientists enjoy the sport all the same, and perhaps it is a celebration of random uncertainty as much as anything else.
You seem to have missed the point of the “Let’s use them to build Narratives” line.
The World Cup is not popular DESPITE having a fairly random outcome.
The World Cup is popular BECAUSE it has a fairly random outcome.
The point of the World Cup is not to find the best soccer team. The point of the World Cup is to build a strong shared narrative.
In this case, much of the strength of the narrative being built comes from the integration of unexpected events. More of the strength comes from the interaction between the narratives of the stadium audience, and the live team as random events occur.
Perhaps this is why introducing random events into tabletop RPG’s is effective.
Sure, football is more unpredictable than other sports, which is what fan like in it as others have pointed out. However, it is patently not true that it can be reduced to noise, otherwise you would have had teams like USA, Ghana, or Japan win a world cup or two, but you did not.
You have a fairly small number of teams which tends to be the best, Brazil, Italy, Germany, Argentina, and those few together have won most of the world cups (15/19 between them, 13/16 if you only consider post-WW2 era). That does not look like random noise by any means, even if occasionally Liberia may beat Brazil.
Yes–many comments are noting the embrace of unpredictability. But do not mistake my point: nowhere do I say that any two teams have an equal chance of winning! See the post by Brian Mingus for an idea of how to reconcile the Poisson noise with increased likelihood of better teams winning the series.
If I had said that the sport “can be reduced to noise,” then my table would be full of 50% values. Better teams are more likely to win, just not with as much certainty as I myself would like.
Your fundamental assumption is wrong. There is very little that is random about soccer, especially at the level of the World Cup. You state that you attended a game and didn’t have any sense of how events were connected. That is your ignorance, and it is a scientific sin that you have carried this forward as your “thesis”.
Imagine it another way. To some people, certain types of music are “noise”. That is their observation, but it has nothing to do with the construction or performance. Others, trained, can easily interpret the music, even when a performer plays a wrong note.
You really have wasted your time.
hmmm…so what would be the scattering cross section for turnovers, or say goals for shots? I would conjecture there is only two observationally significant stochastic processes at play.
Thinking about it as an interaction, every possession either scatters into a shot on goal or a turnover. Furthermore each shot on goal scatters into either a goal, a possession change, or a possession return.
The salient statistical questions are then: Is there a statistically significant difference in the reaction rates between teams? And are the reaction rates specific to each pair of teams, or can they be found by (roughly) taking the product of the independent rates?
The first question is relatively easy to answer given a possessions database for a season, and you have presented some preliminary evidence to the negative. The second question would be much harder, as a single season poorly samples the available random variables (low replication count for instances of pairs of teams playing each other).
A couple things that might be missing from your hypothesis (sorry for my broken english):
A) The influence of home/away crowds in the players and in the referees exists and it is not negligible (a lot more games are won in home ground),
B) In fútbol, when one side is winning the posession is not always geared towards scoring another goal, in many circumstances the game changes from attacking to preventing the other team from scoring (even wasting time)
So, if a large goal difference is not needed most coaches will make substitutions according to the score, often changing an attacker with a midfielder and also changing the positions of the players, so a game between a powerful A team and weak B team might have very different outcomes if it happens in group stage (goal difference might matter, more incentive to large scores) and in the latter stages (only winning matters, there´s more incentive to shut down the game when winning).
Those are two further excellent hypothesized interaction mechanisms, which a detailed possessions databases would be able to test.
Does anyone have a minute by minute possessions database for any team ball/puck/projectile sport?
Excellent points. The home advantage is present indirectly, in that it boosts the expectation value of the home team. But it can still follow Poisson statistics thereafter. All the same, the advantage alters the “test” of which team is fundamentally better. The second point is certainly not represented in my approach, and is a good observation of something that will distort scores, narrowing the natural distribution.
This is just attacking a strawman. No fan thinks that a single game can “prove” a team superior, or that there’s no luck involved at the world cup. There’s obviously tons of luck, which is part of what makes it exciting- it wouldn’t be much fun to watch Germany and Brazil mechanically grinding down every other country over the course of a 100 game series.
That said, if you want less “noise” there’s an easy way to see that- look at the club level, where teams play 30-40 games over the course of a season. At the end of the season, you do have a pretty good idea of how they rank up (although of course injuries and other changes over the season make a big difference).
Personally part of what I like about soccer is that it’s so resistant to stats. In “American” sports, if you know all the relevant statistics, you can predict really well how a team’s season will turn out- you don’t even need to watch the games. But stats like goals per game or possession just don’t tell you much about soccer- you still need to watch the games and use a more holistic approach to understand what’s going on.
As to your first sentence: possibly. As to the second: to the extent that you are correct, I am happy with this, and we are in perfect agreement that a single game’s score should not be taken too literally as ultimate truth. As Gabriel suggests above, it may be that many Americans are especially prone to reading to much meaning into a final score.
You know I’ve always considered your analysis, Tom, and your needs. Now you have to consider mine. No player is greater than the game itself. It’s a significant game in a number of ways.The velocities of the ball, the awful physics of the track. And in the middle of it all, men playing by an odd set of rules. It’s not a game a man is supposed to grow strong in. You appreciate that, don’t you?
I think you just nailed the reason for the popularity of soccer. If sports were predictible, nobody would watch.
You are basically correct. In soccer, the best team doesn’t always win. It is a truism of the sport, in fact.
However, i think your numbers are a bit (way) off, as otherwise there would be far more randomness in the distributions of championships (not just in the world cup, but also league play).
But remember – the randomness is what makes it attractive to the sport’s fans. The crushing portugal goal came out of nowhere, and because of that, its emotional impact was huge. Nothing like it in any other sport.
Embrace randomness! Embrace the void! Embrace the World Cup. (Official motto, 2018 FIFA world cup)
What the statistical probability analysis misses is the human aspect of the sport. There are people making decisions and using very high levels of skills to make things happen on the field. Saying its a Poisson process misses all that! You could reduce all human interaction, including scientific discovery, to some weighted random process, but boy would that be depressing.
Hi Kev! Granted, it’s a complex game that requires mental gymnastics and strategery. But it can still be Poisson. The skills people bring to the game may serve to raise the expectation value, but do not necessarily change the probabilistic nature of the game. The mental processes become join the other random inputs. So I don’t see an incompatibility. It can still be Poisson and have admirable aspects.
Depressing or not, science and life in general indeed enjoy substantial randomness. In soccer analogy, a Nobel Prize is sort-of-like scoring a (big) goal. Sure, talent increases chances, but you and I both know Nobel-caliber people who will never happen on the right discovery, and Nobel winners who perhaps owe more to being at the right place at the right time than to sheer ability.
Random can be enjoyable, and many commenters say as much. My main point was that an individual soccer game is a poor measure of relative capability. Again, many fans responded: well, duh.
Hi Tom! I agree, soccer is a Poisson phenomenon, and a single match does not well measure the better team. What I disagree with is the conclusion that it makes it uninteresting to watch. 🙂
My biggest problem is this:
“This would impact independence, but I can think of lots of scenarios in which it would go either way, so will not bias in one particular direction.”
The reality is that there are factors that cause deviations from expectation that are not random. Futhermore, they might be completely intentional and planned.
A weaker team might find a way to get a result by doing a very specific action, like man marking a specific player or moving back a midfielder, etc.
A team that is not prepared mentally and tactically to chase a game might have a string of 3-0 victories but then loses 1-0 because they don’t know how to come back from a goal down.
A dominant team has won everything that there is to win and simply doesn’t care anymore.
A team knows a specific player in the opposition is prone to temperamental outbursts and baits him into getting a red card.
A team chooses to play a home game in a stadium located at an altitude of 12000 feet, starving the opposition of oxygen.
Those factors might evade statistical analysis but they’re not necessarily random.
And that’s why soccer is more exciting than grindy, statistical games like baseball.
Hi Tom,
I agree with Victor. Although your model is sound, the teams work very hard to strategize to maximize their expectation values (X). Much of the joy I derive in watching sports is to see each team’s strategy, i.e., how they’ve chosen to attempt to increase X. In fact, you could consider each match a display of how they’ve attempted to increase X. One beautiful result of this outlook is that the values of X are unknown until the match is played. That makes the match exciting.
I’m not that familiar with soccer, but American football is chock full of strategy. A team with a star wide receiver might exploit a rookie safety to score more touchdowns (increase X). A defensive line might pile up on the star tight end to make sure he doesn’t get open (decrease the other team’s X). These strategies are often kept secret until they’re tried on the field.
Of course, randomness often gets in the way. Poisson fluctuations can nullify a team’s hard work on the practice field. However, here’s a separate point: a lot–not all–of the events that could be called random (whether it’s raining, a field goal bouncing off the uprights into rather than out of the goal posts, an errant whistle from the crowd) can be controlled for with practice. Quarterbacks practice throwing wet footballs, and coaches change plays from passes to runs in bad weather. Kickers practice to try to get the ball between rather than on the posts. And teams practice with simulated crowd noise. Maybe it’s harder to control for similarly “random” events in soccer.
Thanks for the thought-provoking exercise!
Evan
Hi Evan,
“One beautiful result of this outlook is that the values of X are unknown until the match is played. That makes the match exciting.”
And I would say that the X values are still unknown after the game is over. If the game is not a tie, we have a better sense of the true values, but so poorly that we may even infer the wrong ordering.
As many comments above echo, watching the execution of strategies (aimed at increasing your X or decreasing your opponent’s) is stimulating and a large part of the enjoyment. Many fans are less disturbed than I imagined by the lack of statistical rigor in the (seemingly all-important) final score.
Well I hate football(french) deeply, I tryed to get into it many times for my friends, both playing and watching, resulting in almost deep sadness states especially while watching AND agree with all the mathematical reasonning I think you missed the whole thing.
Football is more a social thing than a sport, to start with when not mediatised it’s about toying with a ball, it’s pretty technical and fun, especially for youngsters but it’s not even the point of my post, nor yourz, hence you criticise it as a spectator. (so it’s about organised / watched football)
You seem to be very educated, you should start to understand that some people do not bother conceptualising things. French football is terrible, teams are horribles, some years 0-0 are more common than anything in leagues. It doesn’t make the action of watching and supporting less social. Even if football as an organised game thanks to you now scientifically sucks it doesn’t suck for everybody. You should respect people, even those with lower “mathematical finesse”. They are also averagely more happy than you and do not suffer particular life imparing handicaps; stop daring implying that masses are mentally hill. Some of game watchers are just here to joke around the match in pubs, have a reason to drink a bit more, it’s a social thing.
Why not doing calculations about that too? What is the most saddening thing about football is the hoolygan syndrom that breaks social barriers in a very disturbing way.
I could read your paper. I could, really, but I won’t.
“But what is the truth of the situation? If team A were to play team B many times, what would the outcomes be? In this hypothetical situation, we want to compare the teams as they are at one moment in time, ignoring fatigue, changes in roster, injuries, evolving strategies, etc.”
So, you want to analyze football by.. Taking what makes it football away?
Way to go, man.
If you read on, you’ll see that this is a mental construct to get at the question: to what extent does the final score of a game (a real event that really is part of the sport) reflect the actual capability of the team at the time of that match?
I don’t think the Poisson model fits, because goals are not independent events. This is a game, i.e. teams adapt their strategies to their objectives and the current game state. In general, the primary objective not to score as many goals as possible, but to win, i.e. to score at least 1 more goal than the opponent. So the winning team wants to slow the game down, i.e. reduce the noise level, and the losing team wants to accelerate it. Since the team that scores first is more likely to be the better team, i.e. the one most able to impose its own agenda, I suspect the true goal distribution has a lighter tail than Poisson. One could test this by checking the distribution of the goal difference.
I remember years ago in the news a story about a guy in Ontario who was a loser socially. He had not much interpersonal skills nor friends, and lived in an empty apartment with not even furniture. He made his money playing the sports lotteries, and was smart enough to figure it out and explained that it’s actually quite predictable, statistically, who will do better in the season results. I know that this is actually in agreement with what you are saying, that it’s all about statistics; I’m not disagreeing. Anyways, this guy became a millionaire based on his educated betting, but spent none of his money since he had zero interests, enraging average middle class folk with families who were working hard to make ends meet. After this came out the lottery company changed the rules and imposed position limits so that it wasn’t possible to win millions anymore, on the grounds that this guy was not playing in line with the spirit of the game, which was apparently not to win, but to have fun at essentially random betting…
What I find more interesting about sports though is what it reveals about our primate ancestry. It kind of spoils the fun to pick it apart like that but I can’t help but notice how organized national sports events are basically just symbolic wars between competing tribes whereby no one actually gets seriously hurt, usually, and everyone returns to normalcy afterwards. It’s generally an anti-climactic outcome-driven event involving getting some small object to go into a hole, which is probably why males tend to get so worked up over it… it’s “about the destination, not the journey”. As you mention, soccer has little build-up to the goals, as most of them seem to be random fluke events combined with varying degrees of skill intended to slant those odds. Kind of metaphorical to the average male’s drives and fantasies…
And what’s even funnier is that more and more these days, the players themselves have nothing to do with the tribe they’re fighting for. They don’t come from there and therefore the only thing they represent is how much money the members of that tribe are willing to fork over to support that player’s salary. All in all, I’d say organized spectator sports is not just a waste of time, but it’s a handy diversion tactic for our leaders to take the spotlight away from themselves and instead focus it on totally irrelevant fictitious wars. Not only that, but it’s a also a very effective way for politicians to whip up tribal nationalism and help get the populace to accept policies (wars?) that otherwise would not be very popular… just look at all the analysis that goes on with sports, and it’s generally of very high quality and scrutiny — people actually take it seriously. If people allocated even a tenth of the neurons they do to sports instead to questioning our leaders, I think the world would be a much different place.
If soccer were deterministic, why would anyone watch? It’s the noise that makes the game.
Anyway, back to the end of the world as we know it…