[An updated treatment of some of this material appears in Chapter 13 of the Energy and Human Ambitions on a Finite Planet (free) textbook.]
A common question I get when discussing solar photovoltaic (PV) power is: “What is the typical efficiency for panels now?” When I answer that mass-market polycrystalline panels are typically about 15–16%, I often see the questioner’s nose wrinkle, followed by dismissive mumbling that 15% is still too low, and maybe they’ll wait for higher numbers before personally pursuing solar. By the end of this post, you will understand why this response is annoying to me. At 15%, we’re in great shape: it’s plenty good for our needs. Let’s do the math and fight the snobbery.

A close-up of a polycrystalline photovoltaic (PV) cell, showing blue tint and a patchwork of crystal domains.
First, let’s look at the efficiencies of other familiar uses of energy to put PV into perspective. I will act as if I’m directly addressing the PV efficiency snob, because it’s fun—and I would never be this rude in person. This may not apply to you, the reader, so please take the truculent tone in stride.
Snark Attack
So 15% is far too low for you? Perhaps you reason that laboratory prototypes and expensive spacecraft applications can get 40%-plus results, so let’s not take the plunge prematurely, given the abysmal 15%.
Perhaps you drive a car. Maybe you’ll stop when you realize that it converts thermal energy from burning gasoline into locomotive power at an efficiency around 15–25% (and this on a finite resource). We should wait for better.
Electric cars deliver battery-stored energy to the wheels at something like 85% efficiency. Now we’re talking. But the charging process imposes another 85% efficiency, and the real kicker is that the fossil fuel (or nuclear) plant supplying the electrical power is only 35% efficient for a net fossil-to-wheels efficiency around 25% (same ballpark as the gasoline car).
Hydrogen fuel cells offer no efficiency advantage in practice, achieving 20–40% for the round-trip hydrogen conversions, not including the efficiency of creating and delivering the electrical power to drive the formation of hydrogen.
If you’re low on energy, you might consider eating. But on second thought, our metabolic efficiency of converting chemical energy into mechanical output is similar to that of a car, so why bother? Turn up your nose.
Perhaps you are a fan of biofuels. This is perhaps the best apples-to-apples comparison to PV, being solar-driven. An Iowa corn field captures solar energy at a paltry efficiency of 1.5%! Okay, but we know by now that corn ethanol has a number of problems. Algae can be far more efficient, right? But even here, photosynthesis tops out at something like 5–6% efficiency under ideal conditions.
PV is Actually Rather Remarkable
Considering this last point, I think it’s rather impressive that we beat biology by a factor of 3 in just a few decades of effort (biology had much longer to work on the problem). Moreover, 15% is perfectly adequate for our needs, as we’ll see at the end.
Qualitative assessments aside, it is rewarding to understand the origin of PV efficiency, and to appreciate that we’re not terribly far from the theoretical limit. The point is that we shouldn’t hold out for some arbitrary efficiency before we embrace solar PV: we don’t really need the extra efficiency, and in any case, physics has something to say about how high we might expect to go.
PV Basics
A photovoltaic cell is most typically a slice of crystalline silicon 200—300 μm thick. (μm = micron = micro-meter = one-millionth of a meter). The construction can either be monocrystalline—slowly grown from a large single-crystal boule, or polycrystalline, cast in an ingot and with a patchwork of crystal domains in varying orientations (translation: pretty to look at). Monocrystalline varieties have a slight advantage in efficiency: like 18% vs. 15%. The cell is doped into what we call a p-n junction, which is basically a diode. What is important here is that the junction is very near the front surface of the cell, and it is here that energy is effectively harvested.
It works like this: a photon of light comes in from the sky, penetrating some depth into the silicon. If it has enough energy (imagine a sign out front: “you must be this tall to go on this ride”), it can pop an electron out of the lattice, leaving a “hole” behind.
The Big Hit: Spectral Limit
This is all we need to know to take our first stab at an efficiency expectation. The first piece of knowledge is that photons below a certain energy cutoff called the bandgap energy (1.12 eV in silicon; corresponding to a wavelength of 1.1 μm) are not absorbed by the material: they sail right through as if going through clear glass. Second, the photons that are absorbed only need to have 1.12 eV of energy to liberate an electron out of the lattice. Any extra is wasted, popping the electron out at high speed. It rattles around the lattice, depositing its “sugar-high” as heat as it calms down.
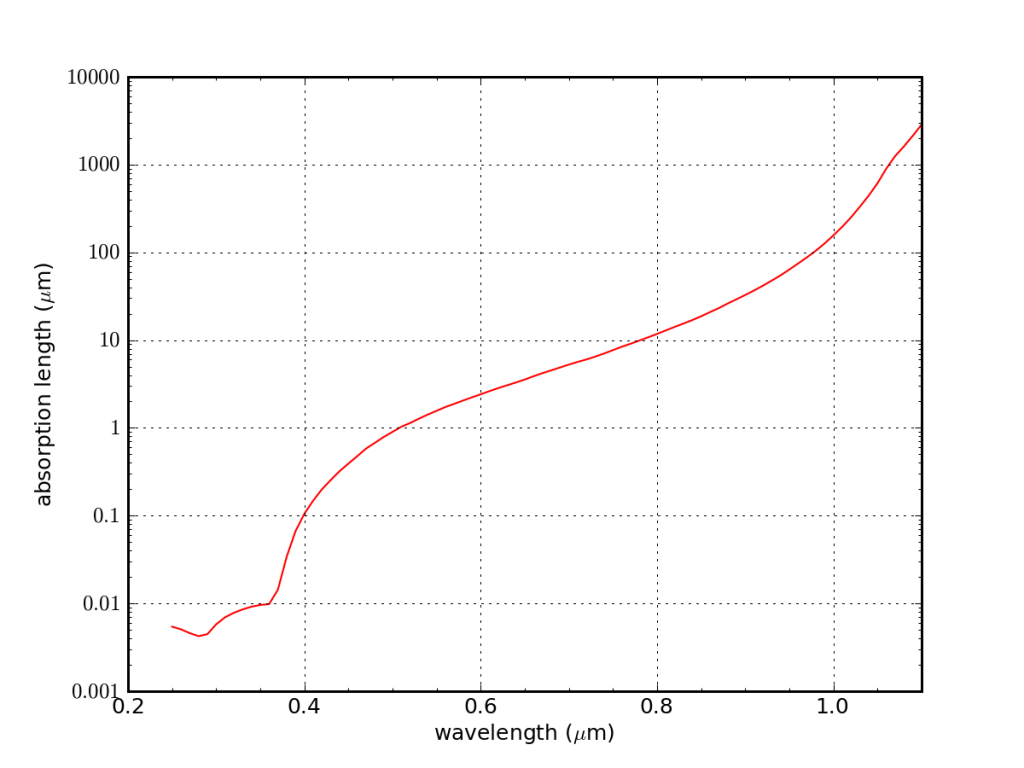
Putting these together, we can say that if a perfect blackbody solar spectrum is incident on the PV cell (ignoring atmospheric effects on spectrum), we lose 23% of the light to infrared transparency beyond 1.1 μm, plus a thermal loss that increases with increasing photon energy (shorter wavelength). The net effect is that we get to keep 44% for PV energy production. This ignores many other real physical limitations that we’ll address below, but it at least represents an upper limit to efficiency expectations.
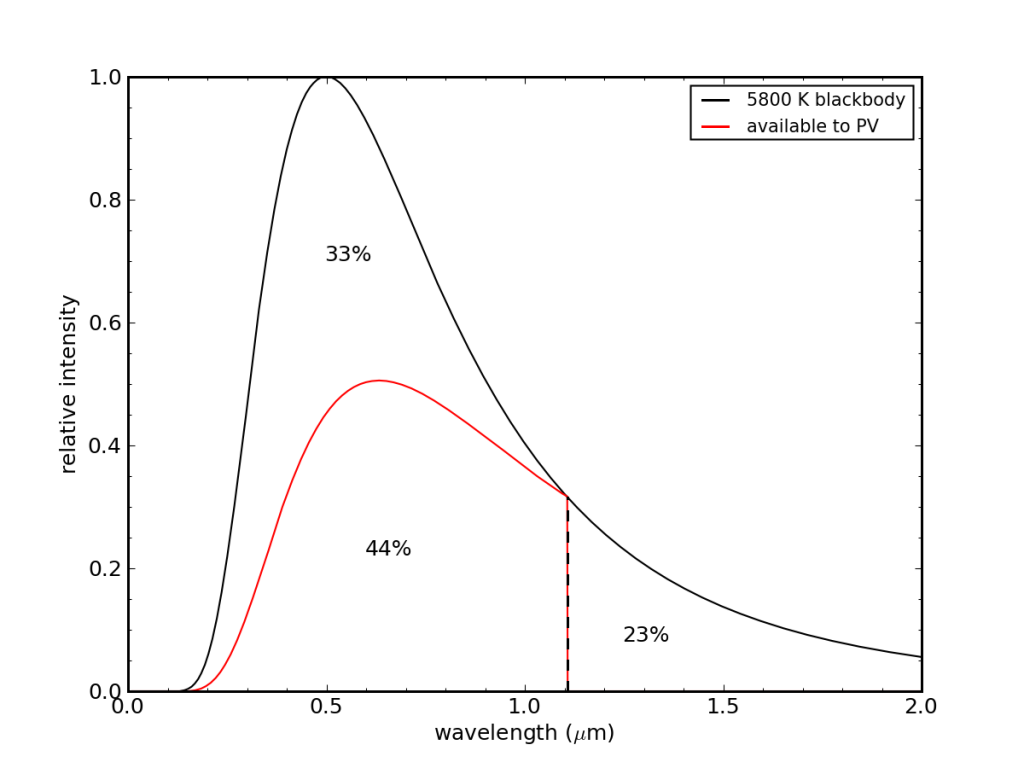
Considering only photon energy effects, a silicon PV cell ignores 23% of the incoming energy, and wastes 33% in light that arrives with more energy than can be utilized, leaving at most 44% available.
We see these effects in the figure above. At 1.1 μm, the photon is well-matched to the necessary energy for liberating an electron, and we use 100% of its energy. As we go to shorter wavelengths, a smaller fraction of the photon energy is utilized, resulting in 33% of the incident energy going to waste heat.
So this most basic analysis indicates that we are doing reasonably well to capture 16% efficiency out of a silicon PV cell when the crudely-determined upper limit is 44%. This is not much different from cars or power plants, in terms of how far below the theoretical thermodynamic limit we achieve in practice.
Better than Silicon?
As an aside, the bandgap energy of silicon is 1.12 eV, corresponding to a wavelength of 1.1 μm. Other semiconductor materials have different bandgap energies. Why restrict ourselves to silicon—even though it is very abundant and we benefit from substantial knowledge and experience via the computer chip industry and related enterprises? I was curious to know what would happen to our 44% theoretical efficiency calculation if we allow ourselves to pick any bandgap.
If we decrease the bandgap wavelength, we squander more infrared light, but use the visible-light-dominated portion of the solar spectrum more efficiently. Longer wavelength bandgaps mean more photons are available, but achieving lower efficiency at visible wavelengths. Where is the balance?
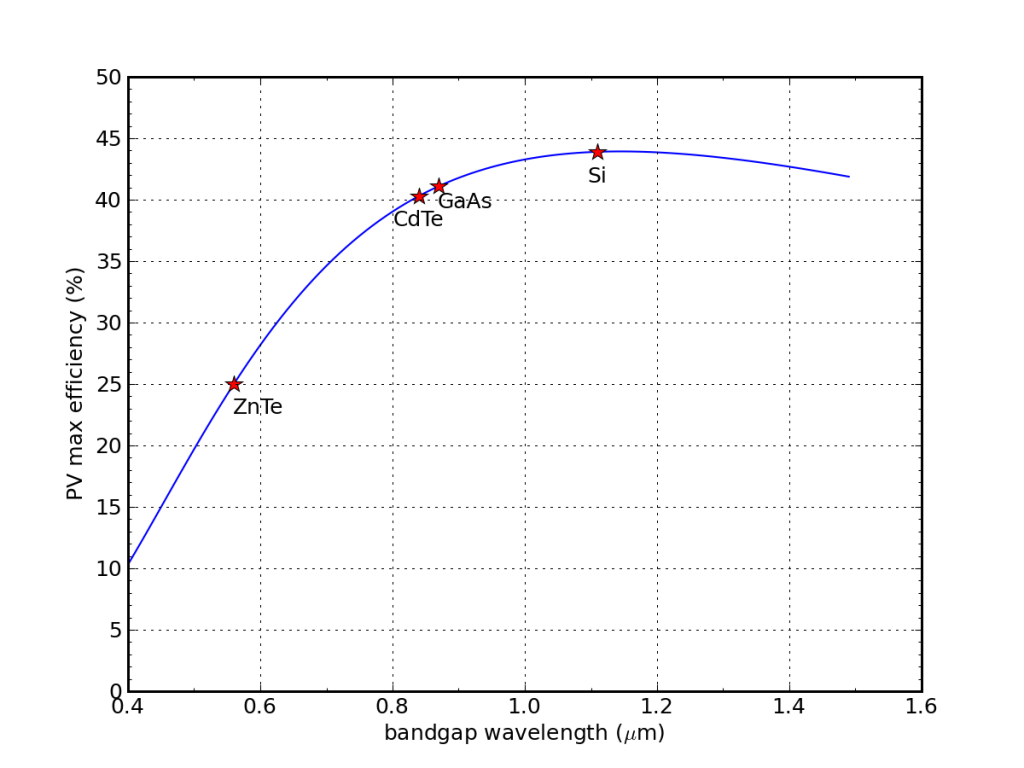
Considering only spectral losses, silicon sits near the maximum possible efficiency, compared to other common PV materials.
I was amazed to see silicon perched near the maximum efficiency position in this trade-off. Who knew? A more careful treatment—using the spectrum as received on the ground and effects like those explored below—finds the peak performance closer to 0.9 μm (1.38 eV), at around 34%.
Into the Weeds: Other Pernicious Limitations
A word of warning: we’re about to get into the nitty-gritty here, so if you’re already feeling a little queasy, there won’t be much harm in skipping to the last paragraph in this section.
Thus far, we have only considered the effects of the input spectrum for a single-bandgap device. But other physical limitations are at play, relating to where (or if) the photon is absorbed, the path history of the generated electron and hole, surface effects, etc. Here are four effects to consider (not a complete list):
- The expected penetration depth of the photon into the silicon depends on wavelength/energy. Photons near the bandgap can travel a very long way before being absorbed, while high-energy photons are absorbed practically at the front surface.
- PV cells are often fabricated with a reflective back surface (also acts as the electrode), so that photons passing through the entire wafer still have a chance to be absorbed on the rebound trip. The reflective barrier also reduces heating from infrared light that otherwise would be absorbed at the back of the cell.
- The p-n junction is at a finite depth, so the photons absorbed above this are far more vulnerable to surface loss.
- Shorter wavelength light suffers more reflection loss at the front surface than longer wavelengths, which is what often gives a blue tint to PV cells.
Absorption length (data from this site) is shown in the logarithmic plot below. This is only the characteristic depth of absorption, but the profile at any given wavelength follows an exponentially decaying probability of absorption, set by this scale.
At a wavelength of about 0.5 μm (green light), the absorption length is about 1 μm. Shortward of this, the third effect enumerated above becomes important. Longward of a wavelength of 1.0 μm, the absorption length becomes > 200 μm, and the light often reaches the back surface, where factor 2 comes into play.
After the absorbed photon creates an electron-hole pair, the electron wanders about, bumping this way and that, with no direction in life (diffusion). If it happens to run into the p-n junction near the front surface, it gets swept across toward the front, where it joins a flock of eager electrons itching to run out into an external circuit and do some work. If it wanders off the other way (deeper into the crystal) it may never find the junction; eventually re-combining with a “hole” elsewhere—often facilitated by crystal grain boundaries and surfaces, or by defects and impurities in the crystal.
Likewise, a hole generated above the junction may wander into the junction and be pushed to the back, in an arranged marriage (recombination) with an electron returning to the back side of the cell from service in the external circuit. The junction therefore acts like a pump, pushing electrons one way and holes the other—encouraging them to participate in a flow of current through an external device.
I made a simple model to account for these effects, where the probability of being “pumped” is unity at the junction, tapering linearly to some lesser probability at the front and back surfaces (pf and pb, respectively). Linear makes some sense, because—as I had to prove to myself via simulation—the chance of a random walk bumping into one extreme or the other is just linearly proportional to its starting position relative to these two boundaries. If the junction always sweeps the charge, cashing in its energy, while the surface has some fixed probability of gobbling up the charge and thus forfeiting the energy, the probability relation for points between is linear. This ignores internal recombination along the way, which dis-favors long-haul paths, making the back surface “hungrier.”
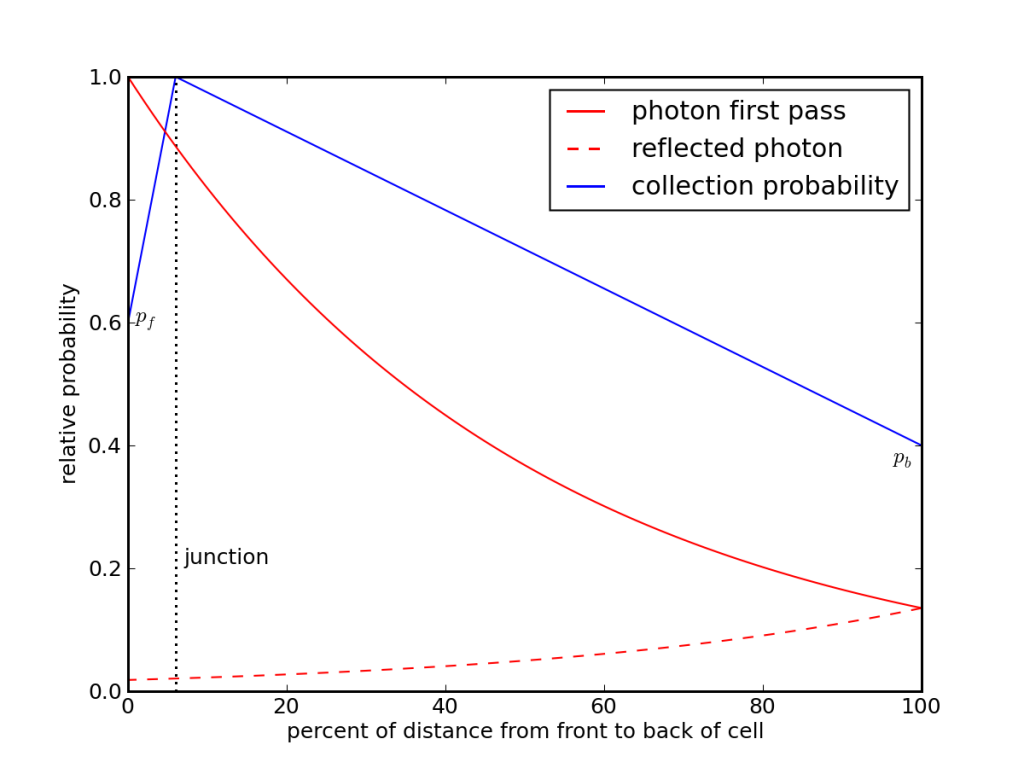
Model for evaluating conversion probability as a function of depth and penetration, ignoring bulk recombination losses. For a given wavelength, the absorption curve (red) is multiplied by the collection probability (blue) and integrated through the bulk. The front and rear surfaces have some probability of gobbling charge carriers that bump into them. The junction is actually much closer to the front, but is set back a bit for clarity.
Folding this effect together with the exponential absorption probability vs. depth, and allowing perfect reflection at the back, I can produce an expectation that accounts for the first three factors above. I don’t explicitly cover the front-surface reflection loss. Most new photovoltaics have an anti-reflection coating that reduces what would be a 30% surface reflection to just a few percent across most of the visible and near-IR band. But it gives out at the blue or near-ultraviolet end, allowing the reflection to creep back up to 30%. Since the PV response at the blue end is weak already due to surface losses and poor utilization of photon energy, I just absorb the extra reflection loss into the front-surface gobble probability, which is relevant primarily for short wavelengths because of their tiny penetration depths.
Okay—boy are we in the weeds here: let’s try to pull out. Putting these effects together, we get an expected efficiency of a silicon PV of 35%: not far off from other evaluations. Thus the real devices are in fact getting within about a factor of two of the theoretical maximum, which is better than we get in a lot of other, important domains.
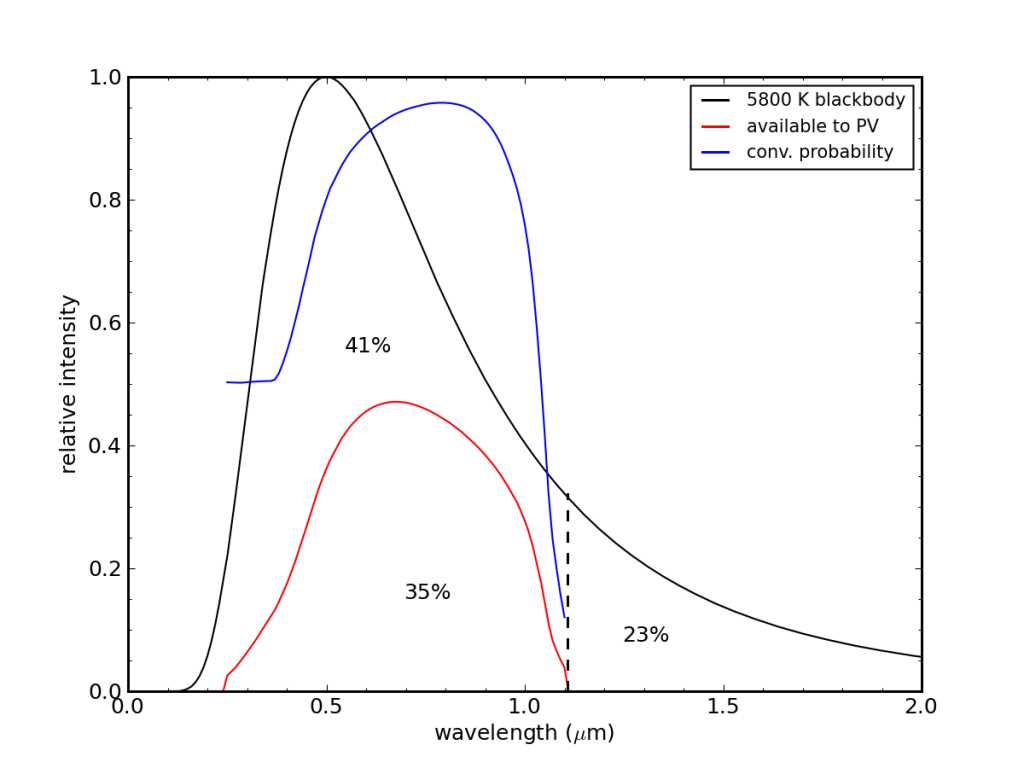
Including absorption length and surface losses, the maximum possible efficiency drops to 35%, when front and rear surface probabilities are set to 0.5. Bulk recombination is not considered.
The modified curves appear above. I have added a curve for the probability of conversion. Now the photons close to the bandgap mostly sail through the device, even given a second pass due to the reflection at the rear. We get high probability between 0.6–0.9 μm because the light is converted to an electron far enough from the back face, but we are not yet suffering from the front-surface inefficiencies. The probability settles out at the 50% level for short wavelength, which I arbitrarily assigned as the gobble-factor of both the front and back surfaces. The 35% result can range from 28% to 41% as I change both front and back gobble factors all the way from 0% to 100%.
In summary, we have reduced our initial 44% expectation to something in the neighborhood of 35% by considering physical processes that are practically unavoidable. We could continue this trek, accounting for all the physical phenomena that lead to 16% efficiency in practice, but I think I have already overdone the point: that there are really good reasons why the efficiencies will not climb to arbitrarily high values. Basic physics stands in the way, and I am left impressed with what we’ve got.
A Fantastic PV Tutorial
After developing the analysis above, I came across a great site explaining the fundamental physical processes involved in photovoltaics. The abundant interactive graphics are especially delightful. For the parts with which I am familiar, I find the information to be reliable and accurate. I was especially pleased to see confirmation of the collection probability scheme I implemented (you get the same linear effect in the interactive simulation if you neglect bulk recombination by increasing the diffusion length and crank up the surface recombination effect).
PV Shenanigans
How is it that some lab tests or expensive spacecraft PV panels do better than the theoretical maximum calculated above? Most often, these are multi-junction devices. If we form a stack of PV junctions made from materials other than silicon, each with a different bandgap, we can more efficiently utilize the spectrum. We’d put a thin layer of material with a blue bandgap up front, followed by a green-bandgap material, and maybe silicon underneath. The longer wavelengths will sail through the first two layers and get used by the silicon. The short wavelengths, which had trouble in silicon, are more efficiently tapped by the layers in front. More of the photon energy goes into liberating the electron rather than into its velocity (heat), and more of the photons are captured.
Such devices are certainly possible to make. They are more complex, require less standard semiconductor materials, and can therefore be very expensive. For a satellite, the cost of the panels is a trivial fraction of the total cost, and launch mass means everything. So it’s worth paying a premium price to meet their power requirements in a smaller panel. For large-scale deployment, we’re likely to go cheap and low efficiency. In fact, it is more likely that a massive deployment would use thin film (amorphous silicon, e.g.) devices, which typically have efficiencies lower than 10% but are easier to mass-produce.
It Comes Down to This
This brings us to some practical matters. Returning to the PV efficiency snob, efficiency effectively maps to area. A typical location within the U.S. gets an annual average of 5 full-sun-equivalent hours per day. This means that the 1000 W/m² solar flux reaching the ground when the sun is straight overhead is effectively available for 5 hours each day. Each square meter of panel is therefore exposed to 5 kWh of solar energy per day. At 15% efficiency, our square meter captures and delivers 0.75 kWh of energy to the house. A typical American home uses 30 kWh of electricity per day, so we’d need 40 square meters of panels. This works out to 430 square feet, or about one sixth the typical American house’s roof (the roof area of a two-car garage). What’s the problem?
If the calculation had yielded six times the roof area, or even one times the roof area, I would see the problem. There is even a problem with one-half, or one-third, since finding a suitable portion of roof facing the equator is an issue. But at 1/6, most houses can hack it (barring shade trees, in which case it’s not better efficiency you need!). Tripling efficiency to 45%, if even possible, would translate to 5% of your roof footprint. But there’s no magic in that. We’re already to the point where it’s feasible and practical from an energetics/area point of view. Stop crinkling that nose!
In fact, we can extend this argument to the nation or world as a whole. Even at 8% efficiency (typical thin film multi-junction device), we could generate all primary power with a minor land footprint, as the picture below shows. Efficiency is not the bottleneck. It’s usually price. And more complex, higher purity, higher efficiency cells don’t usually lower the price.
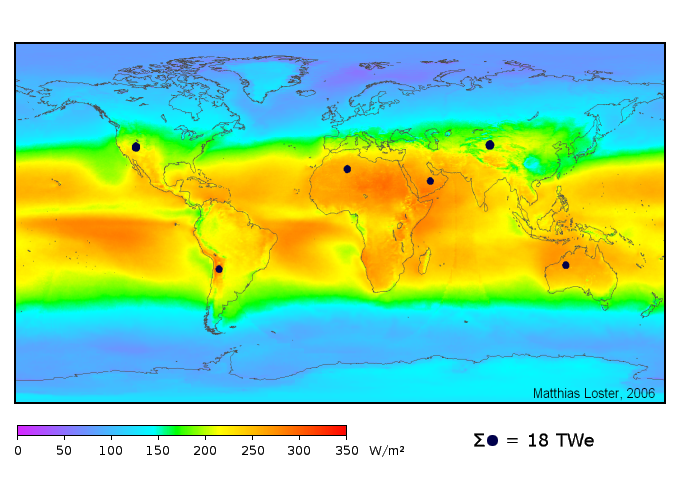
The land area needed to produce 18 terawatts (50% larger than 2010 value) using 8% efficient photovoltaics, shown as black dots. Source: WikiMedia.
We do not lack the area/resources on the planet to get enough energy from PV, even at half the current silicon efficiency. Other alternatives come nowhere close to being able to make this claim. As a side note, because North America uses 25% of the world’s energy at present, its dot may need to grow a bit, but not exorbitantly.
As reassuring as this picture is, the photovoltaic area represents more than all the paved area in the world. This troubles me. I’ve criss-crossed the country many times now, and believe me, there is a lot of pavement. The paved infrastructure reflects a tremendous investment that took decades to build. And we’re talking about asphalt and concrete here: not high-tech semiconductor. I truly have a hard time grasping the scale such a photovoltaic deployment would represent. And I’m not even addressing storage here. So while it’s physically possible, and the efficiency is sufficient to allow it, it remains a daunting challenge.
Could we even get started? Would we agree it’s the right path? Would it have much leverage against oil, given that it’s not a liquid fuel replacement? Will it always seem dreadfully expensive after being spoiled on ridiculously cheap fossil fuels? Once oil is in global terminal decline, economies will struggle to cope, and this may not seem the most opportune time to strike out on an unprecedented large-scale expenditure, whose costs and benefits will be debated hotly.
Have I ever mentioned that an easy solution is a voluntary reduction of energy demand? But this doesn’t sound like expansion/growth, so how would that idea ever gain traction?
Hits: 12694
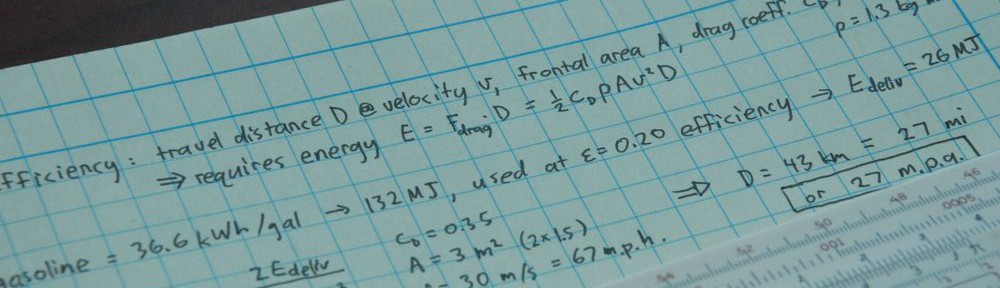
Question: Are PV cells following the same trajectory as other silicone chips, i.e., Moore’s law?
No. As Tom states in his article, there is an upper bound on PV efficiency. Consumer grade PV efficiency has been basically flat for years. Slowly increasing, but nothing drastic like Moore’s Law where computing power doubles every 18 months or so.
What really matters is cost per watt – space is rarely an issue – but how much it costs to buy enough panels usually is. And that has also been decreasing as manufacturing capacity goes up.
You’re setting yourself — and your readers — for the “all or nothing” trap that utilities exploit repeatedly. Would it be nice to achieve 100% power from solar? Sure, but solar — and other renewables — can make an important contribution at far less levels. Which is better? Consuming coal at today’s rate or at 3/4ths or 1/2th today’s rate? There is a proposal in Europe called Desertec to use Solar Thermal (not PV) in the deserts of North Africa to provide power. While still just a proposal, it offers some provocative ideas about what is achievable.
I would think I’m stating the opposite: don’t get hung up on 15% as a low number. It’s fine. This article says we’re good to go right now, from an efficiency standpoint. Let’s do it!
[shortened by moderator]
When I began reading this article, I sincerely hoped that you would show us there is huge progress that can be made in PV. Every few months a news article shows up on slashdot, google news, etc that researchers made a 40% efficient panel. But nothing makes it to market, and hearing your explanation why, I doubt they ever will. I almost got my wish fulfilled when I got to the part stating that only 1/6 the average roof would need PV panel and I looked at the map with the seemingly small dots.
But alas, those seemingly small dots are quite large, much like a car’s passenger mirror distorting the giant tractor trailer that is really only a few meters away despite its appearance. The fact is even worse when you consider how the PV panels would need to be spread. I have a feeling the North American Dot would have to grow immensely to compensate for the United States energy use per capita.
Don’t get depressed that we may not see cheap PV at efficiencies much above 15%. It’s good enough already to be useful. If you think we need 40%, then I hope this post can re-calibrate you to embrace PV at 15%: it’s good enough. Yes, full scale solar requires an enormous area. That qualitative statement would not change even at 100% efficiency.
My concern is that if PV can only exist as 15% relatively cheaply, what are we going to rely on in the future?
1. Fossil fuels – peaked, or maybe soon
2. Hydro – most good places already in use
3. Geothermal – only good at specific places, may or may not cause minor earthquakes depending on the research
4. Solar – need large sq foot to be useful, only good certain locations
5. Tidal – wildlife impact, locations
6. Nuclear – storing spend material, ridiculous high initial cost
And the biggest problem of all. Rising consumption of electricity. It always seems one step forward, two back. More efficient gas engines – larger heavier vehicles. More efficient refrigerators – larger refrigerators, better A/C & heating – bigger houses.
The answer is “all of the above.” The issue is that efficiency IS a problem: the stumbling block is that people think energy PRODUCTION has the efficiency problem, when really, it is our energy USE that has the problem. Both could be somewhat better. Honestly, I would happily cover the entirety of my roof with super cheap solar panels if they existed, as opposed to 1/6 of my roof with expensive ones.
It is certainly possible to go above the limit for silicon cells, in theory (I think the upper limit for silicon is more like 30% because they will operate without concentration of sunlight). Multijunction cells are covered in the article as one route. I’ve written a review of high efficiency approaches that you might find interesing, http://www.modernenergyreview.com/articles/routes_to_high_efficiency_photovoltaic_conversion.html
I don’t think high efficiency is just around the corner but I think given enough time we will be moving in these directions.
Well done, thanks. Have you read Sustainable Energy – Without the Hot Air by David JC MacKay?
Dr. MacKay covers a large amount of ground, literally and figuratively (while based on British parameters it’s still hugely relevant in the US and elsewhere). The fundamental point is that country sized sustainable energy solutions require country-sized installations. I think his manner of presentation and back of the envelope estimation and calculation ties in well with your approach and I believe you’d enjoy it.
Big fan of MacKay and his book. Check it out, people (free PDF version at http://www.withouthotair.com). It’s on my blogroll as well.
Given some of the comments, I have re-written sections of the article to better emphasize that 15% PV is not a problem. It is good enough to do what we need. I want to stop people from thinking that we need to hold out for higher efficiency: physics gets in the way. Embrace 15% as a glorious and useful number. Apologies if this point is now overstated in the article as a result.
An interesting corollary: can we improve photosynthesis? If green plants are on average 3% efficient, doubling efficiency halves the amount of cropland dedicated to food, freeing up half for biomass.
Green plants ignore the a big chunk of the sunlight received (http://hyperphysics.phy-astr.gsu.edu/hbase/biology/ligabs.html). What if we, say, engineer plants to also use rhodopsin and scoop up the spectrum around 540 nm?
Have at it!
Well, the thing is that the main miracle of the plants is not that they tie up energy. Getting that energy is indeed a precondition for what they do, which is creating incredible complex molecules, sustaining life. And we have already stretched crop growing by taking more and more of the useful production. Many believe that we through breeding etc have improved production a lot, but that is actually not correct. We have increased production of what we WANT. So in the field, we have killed off all the weeds, we made the wheat or corn produce much more grain and less stalks and roots (which is also why they get more pests and need chemical fertilisers, that uses a lot of energy for their production) etc. The main way we actually increase biological productivity is by adding some basic natural factor that is missing, most clearly shown by the example of irrigation by which we can make deserts bloom (and deplete water resources, salinate soils etc.). Our common fields don’t have any remarkably higher biological productivity than the wild nature, and if they have they mostly produce less other valuable eco system services. What most people seem to miss is that there ARE quite fixed biological limits for all things. Fossil fuels have spoiled us to believe there are simple solutions – but they are in fact just accumulated solar energy from plants over a long time
Never mind the surface area of roads.
How’s it compare with the surface area of roofs?
Assume the development of a roof shingle / tile / whatever that’s a drop-in replacement for those currently in use today at a cost that isn’t that much more than a standard asphalt / ceramic / whatever one, so that the entire roof surface could be used. What sort of efficiency would we need? I suspect it’s far less than the low efficiency we already have for such products already on the market.
My guess — and hope — is that we’re looking at less than a decade for solar roofs such as that to become the norm. Asphalt will only get more expensive and PV will only get cheaper. Even if a new roof costs twice as much but eliminates your electric bill in the process, it’ll be a no-brainer.
The smart roofing contractors are expanding into the PV business, and the smart PV contractors are expanding into the roofing business.
Cheers,
b&
How much roof space is needed depends on the power usage of the building.
You’ll typically see commercial buildings being able to offset about 25-30% of their usage with a roof-top system.
Most suburban houses are able to offset 100% of their usage with a roof-top system. For example, my house has a 3.24 kW array on the roof which produces about 4.8 MWh / year – nearly enough to offset my annual household usage. But if I really wanted to, I could probably cram 20 kW of PV on my roof. I would probably get about 23 MWh / year out of it, nearly 2000 kWh / month.
Let’s saw I also add 2 electric vehicles to my house driven about 12,000 mi/year each. EVs get about 3.5 mi / kWh from the wall, but that’s still only about 600 kWh / month. Even then I’d easily produce more electricity than my household uses.
@ drees That is along the lines of what I was thinking. Go lower efficiency on the cheapest materials (there may not be enough Si for all the PV cells we would need) and spread them over 100% of the roof. Make every roof top a energy generation station. Use and store what you can at home and then send the rest over the grid.
Commercial is always a dense user like tall buildings in cities (I live in a 7 story condo building over 1 city block of land). If I had a house, I would definitely be looking into thin film shingle replacement system for my roof and home energy storage. I know I cannot go off grid, but if it zeros out my bill or better and gives me a safety net for “situations” that would be worth it.
Then I can spend more money on canned food and shotgun shells. LOL
Wal*Mart goes solar in California.
http://www.tekgoblin.com/2011/09/21/walmart-appeals-to-california-liberals-with-solar-movement/
If Wal*Mart can make the numbers work, it’s “good enough” for large bases. I am confident there are tax credits or subsidies (even good will), but it will drive adoption and aid mass installation companies — an engineering services companies — into the business.
…and of course, a 2-liter soda bottle works pretty well during the day:
http://www.youtube.com/watch?v=JOl4vwhwkW8
The bottle trick is neat. Let’s see: 10 cm diameter collects about 8 W of solar light power. The solar blackbody is close to 100 lumens per watt, so we get about 800 lumens, which is the equivalent of a 50 W incandescent bulb. It works!
I’ve got a couple Solatubes installed in my home — a somewhat more sophisticated and much more expensive version of the same thing. Not only are they plenty bright — I never turn the lights on in the kitchen or bathroom during the day — but the quality of the light is superlative. I’ve got a bunch of SoLux daylight balanced lighting elsewhere in the house (the gold standard in art museum lighting), and even that can’t compare to the Solatubes.
Everybody thinks of solar hot water as the cheapest, best bang-for-the-buck way of getting into solar energy, and it’s certainly an excellent deal. But I think solar lighting is even better.
Cheers,
b&
I’d love your insight on the use of solar energy for power in other forms than electricity.
The comments above were starting to head that direction with solar lighting, but I’m thinking specifically of heating. I believe I read that the typical electric usage of a steel foundry is in the millions of dollars per month, and I’m sure that there are other hi-temp operations that would be similar (glass or concrete production, say, or firing bricks).
How realistic might it be to replace:
fossil-> electricity -> transmission grid -> manufacturing heat
with
solar heat -> manufacturing heat
or
solar heat-> heat transmission grid -> manufacturing heat
?
And separately, how about
solar heat -> heat transmission grid -> household heating
?
Thanks!
Mike
Process heat for manufacturing is almost always direct-source. No fiddling with electricity. Burn coal, gas, oil directly. Concentrating solar can get a medium very hot, but I have not evaluated what it could do for steel processing and the like. My intuition says it’s hard.
You may read this paper by Vaclav Smil about the challenges ahead for one of the most fundamental industrial processes: http://www.vaclavsmil.com/wp-content/uploads/docs/smil-article-20090917-iron-age.pdf
Awesome post, Tom.
I feel like the snobbery has roots in the pervasive Myth of Progress [ http://en.wikipedia.org/wiki/Idea_of_Progress ]. In other words, a lot of people still expect technological solutions to save us – we just need to develop them and then bang we’ll be able to switch to sustainable energy.
To my mind that’s just an extension of the myth of progress narrative. The point explicit in your post is: we HAVE the technology, the technology isn’t the issue. We know what we need to do, we have the ability to do it, we just need to… you know.. do it. But our social consciousness ever since the Enlightenment has been we can do whatever we want and our Science and Tech will allow us to do it.
Ironically enough, I feel like the popular conception of this narrative has led people to totally misunderstand physical limitations and reality. Almost as if we’ve negated any real respect for physics we might have had by our belief in the Magic of Technological Progress. The narrative has perverted real understanding of our reality.
Very well stated. It was exactly these sentiments that prompted me to invest precious time into a blog to bring physics back into the discussion. In computer code, physics != magic. You’ve hit on a key aspect of the problem, too, in that narratives are incredibly important, and our current narrative is severely distorted by our unprecedented discovery of the earth’s million-year battery in the form of fossil fuels: to be spent in the blink of an eye. We need a narrative that puts this in perspective.
So true. The power of narrative is something that has been slowly dawning on me over the past couple years. The monumental question of how do you change a dominant narrative is pretty daunting (and how do you make sure your cure isn’t worse than the disease?).
I do think that the current economic climate is pushing more people to question some of the dominant narratives. I found this article (not a self-link) to really speak to that:
http://nofearofthefuture.blogspot.com/2011/09/day-narrative-died.html
What people don’t appreciate is how “private sector always knows best” ideology has come to dominate any discourse. The profit motive is a powerful force and oftentimes pulls people in the wrong direction. Let’s look at the coal industry. It employs close to 100,000 people and has worked with utilities for decades. In fact, it can be said utilities and the coal industry are joined at the hip. Consequently, any discussion of energy is subverted by the disinformation actively promoted by vested interests. Let’s not be fooled. I currently get ALL my electricity from Wind Power at 9.4 cents per kWh. The fact is the Earth is ALWAYS in thermal disequilibrium. Therefore Wind will exist, it’s just a matter of location. The central US has some of the best Wind resources in the World, but what are the utilities in the Midwest using predominately? Coal and nuclear. Let’s end the Tyranny of corporate multi-nationals (not even “corporate America”) and move forward.
As we all knew, and this article proved, the issue is not efficiency but cost. Get the initial cost down and you would have panels on every roof.
One interesting comment in the article was comparing the amount of space needed for panels for the US rate of consumption, to the amount of space allocated for paved streets.
I proposed this idea years ago – build a stronger panel, and lay panels in all paved streets.
This would have no impact on the environment (ugly panels, shading of desert land) and would make the power available where the people live.
Ok, I understand that this idea is like the bell on the cat, great idea, now who is going to do it?
But is it possible to build a solar panel that could withstand car and truck traffic?
Hmmm????
even if it could withstand a vehicle, AND it could withstand weathering (have u driven on a street in the Midwest that isn’t repaved every 2 years)
you would get ZERO energy when the roads are covered with snow, which is decemember-march in a large portion of the USA. at least u can scrape snow off a roof, u cant do that with snow and the road. where i grew up u dont salt a road u sand it becasue that snows not melting.
The best study I’ve seen on rooftop capacity is an old NREL study that forecasts 600 GW of PV could be hosted on U.S. rooftops. That can probably be increased by a factor of about two if better technologies are developed for imperfect slopes. In addition, we’ll probably start to see sidewalk, roadway and parking lot roof structures to host more panels. That’s still about one third of the overall energy needs of the country, but if you start to add solar farms in the desert, you’ll end up very quickly with all the energy we’ll ever need. The good news is that we have many decades to build that infrastructure, just like we did with the nation’s paved road system.
Does the global requirement of 18TWe include energy used for transportation? If so, it’s encouraging that since 20-27% of global energy goes toward transportation, we could get away with maybe 10-15% fewer TW, assuming we could all accept that we won’t be driving cars everywhere and take electrified public transit instead.
18 TWe more than accounts for transportation. We use about 12 TW total today, and much of this in inefficient heat engines. We may be able to carry out today’s activities at 8 TW or less in a solar world. Won’t be as cheap as fossil fuels, so unclear how we cope with this new phase—or if we even drive in that direction.
Another winner Tom.
After 20 years in the renewable energy business, I have yet to see a better explanation of the efficiency question than this.
I’d be really interested to see you tackle the cost question. I am constantly barraged by many in the utility world that state unequivocally “solar is too expensive, coal is great!”. Figuring in the total cost from mining, rail transportation, pitiful efficiencies of thermal electric generation, transmission losses, and the low efficiencies of most electrical appliances, electric generation from a central plant standpoint is one of the most inefficient ways to get electricity to the public. We generally figure that it takes three KWH of generation to get 1 KWH to the end user. Yet, since Thomas Edison started doing it in the late 19th century, it still hasn’t changed very much. The major difference is AC versus DC, with all of its inherent disadvantages.
While PV costs have come down (dramatically) recently, it’s still difficult to get anyone to pay attention. It’s simply too easy to pay a utility bill without thinking about the future.
It’s also tough to get a true cost estimate for PV modules due to subsidies up and down the supply chain:
http://spectrum.ieee.org/energywise/green-tech/solar/will-the-real-pv-price-please-stand-up
Too true. It’s also equally tough to get a true comparison going with fossil fuels due to their subsidies- overt and hidden. The lack of royalties paid by petroleum companies for drilling on federal land is a good example. Loan guarantees and liability limits for the nuclear industry is another. Additionally, taking the socialized cost of pollution and climate change into account would make the comparison even more interesting.
Comparing efficiency percentages between highly concentrated energy sources like gasoline or nuclear and diffuse energy sources like solar or wind requires a discussion of the difference in exergy between a given source and its environment.
The most efficient use of solar energy is actually for low exergy projects like passive heating of air and water or concentrating to fire a solar oven. Using low exergy sources to do low exergy tasks has to be a big part of the sustainability conversation.
A civilization run primarily on solar energy (and other low exergy sources) will look quite a bit different than one run on fossil fuels because it will always be a luxury to use highly concentrated energy (read: electricity) that has been gathered and stored up from low exergy sources.
Sorry for the overuse of the word exergy but I have found that it is so often overlooked or not understood. And having a firm grasp on the implications makes all the difference in plotting a realistic path to the future.
I don’t mean this as a criticism at all … just an addition to the conversation and the thought process.
Nice work to graphically show how much land area we need for PV to supply our electrical needs. It would also be nice to compare with how much land area we currently use to grow our food (60x more).
Can we not use a solar water heater heat water and then use the heat on the PV to get the electron released off the PV panel ? Is ‘sun rays’ only able to get that release of electron from PV ? Not the heat wave ? If heat wave can, we can stack the PV panels one over another instead of roofing it and then create more power with same square area of available roof area ?
Not a chance. Even at boiling temperature, the characteristic particle energy is 0.03 eV: far short of the 1.1 eV needed to pop an electron into the conduction band. And even if something like this could work, stacking loads of cells does not increase the amount of incident energy available: there is only so much to go around.
California has huge potential for PV on home roofs. We have incentives, just not enough incentives form my point of view. The issues are politically but not technically complex. For me, the key is that one cannot sell the power to the provider. Rather one can only deduct what you generate from your bill. This means, for me at least, much greater incentive for conservation than for investment in PV. Can somebody add or correct my point of view here?
http://www.cpuc.ca.gov/PUC/energy/Solar/.
http://solar.calfinder.com/rebates/California
Terrific blog, especially your posts about limits to growth (closed for comments unfortunately). I have been thinking along similar lines. I have uploaded some material on exponential growth that you and your readers might find interesting, at http://www.slideshare.net/amenning/.
On the question of whether economic growth can continue through “decoupling” of GDP from resource use , I have devised an exercise that goes like this:
*** Consider a model economy consisting of a “material” and an “immaterial” sector. The first manufactures goods such as cars, wind turbines, internet servers, etc., and requires one unit of throughput per unit of output. The latter provides “intangible” services based on knowledge or information, such as online learning, music download, internet gambling, mortgage-backed securities, litigation, etc., and requires zero throughput. Initially, each sector constitutes 50% of the economy and has a total value of 1. Our model economy will grow by 3.5% annually without increasing its rate of throughput, i. e. only the “immaterial” sector will grow. What will the “immaterial” share of the economy be after 100 years? More realistically, assume that the immaterial sector has a throughput efficiency 10 times that of the material sector (i. e. 0.1 units of throughput per unit of output). Calculate the total throughput in this model and characterize its growth.***
This exercise shows, of course, the absurdity of what Herman Daly mocked as “angelic GDP”. There is no plausible way in which indefinite exponential economic growth can be reconciled with the constraints of a physically limited world.
Let’s not forget the issue of energy storage. Grid-tied PV systems are popular now. I’ve heard claims that some PV systems can produce all of their energy needs, but that is only considering the grid as if it were a giant battery. If the grid is completely dependent on fossil fuels, how can a grid-tied system possibly be sustainable in the long term (Post-peak)? If the grid goes down, then a grid-tied system goes dark. I have heard the claims that some grid-tied PV systems generate more energy than they use in the summer and then receive credits for the excess energy fed to the grid. In the winter these same systems draw upon their credits to heat the building. But let’s face it, you cannot heat a building with credits and thus you often will use some sort of stored energy in the form of fossil fuels for your winter heat.
In your comparison between PV systems and biofuel, have you considered that biofuels are a way to not only capture solar energy but also store that solar energy as well? How does the efficiency of PV cells compare to biofuels if you consider the case where you want to use the captured solar energy 6-12 months after the solar energy was captured?
I like to point out that PV panels are not solar energy but rather solar engines. When comparing technologies we should compare apples to apples. PV panels are like diesel generators that have been smashed wafer-thin, placed on a roof and every day (mostly) are fueled by rainshowers of diesel no.2. No wells, no pipelines, no refineries and no Navy-protected seaports. The only backend is the industry that makes the panels, just like an industry makes the diesel generators. With solar-breeder replicators the pv panels can make more panels. Just dig up some silica sand.
Also, those who complain about the intermittent nature of solar power need to understand that most generators on the planet are just as useless at 3 am as the load falls below capacity.
Interesting post but there is a misleading comparison. The theoretical maximum efficiency of a conventional solar cell (single band gap) is around 44% as indicated by the author and calculated using a detailed balance argument (see Shockley–Queisser limit) that assumes a quantum efficiency of 100% and other restrictive assumptions, e.g. generation/recombination events are only radiative. However, the author fails to mention that this theoretical efficiency calculation is based on the premise that the cell absorbs fully concentrated light (see below) and yet the comparison is to that of a conventional cell designed to absorb unconcentrated light. A better comparison would be to assume the conventional cell absorbs unconcentrated light for the theoretical efficiency calculation (apples to apples), which happens to be 31%.
Concentrated light
One of the assumptions used to achieve 44% is that the cell only absorbs photons that have a characteristic temperature of the sun. This is termed “full concentration”. Yes, optics and lenses can increase the number of photons that have a characteristic temperature of the sun relative to the photons that have a characteristic temperature of ambient but not to the extent of full concentration.
Simplifications abound in the post (perfect quantum efficiency, etc.). But concentration is not assumed. The spectrum of incoming light is the only consideration. The spectrum is the same whether concentrating or not. So the fraction of energy lost to sub-bandgap transmission is the same, and the fraction of photon energy that goes to promoting an electron into the conduction band is also the same. I do not understand the language of a characteristic temperature of the sun. The distribution, or spectrum, is certainly characterized by a temperature, but it is not a useful metric for an individual photon. If I had to describe ambient temperature in terms of a spectrum of photons, it would be thermal radiation centered around 10 microns, which is not at all what (even unconcentrated) PV makes use of.
In order to reach the 44% efficiency value, one needs to make the assumption that the incident photon flux hitting the cell’s surface behaves like a black body with temperature of the sun. For the sun as seen from the earth, this photon flux is reduced by a factor of about 4.6 X10^4. See http://ieeexplore.ieee.org/xpl/freeabs_all.jsp?arnumber=5124319 on why the efficiency for unconcentrated light is 31%. I think we are talking past each other…my fault.